Εκθετική συνάρτηση
Μαθηματικά (ΔΕ) (Γενικό Λύκειο)
Στο παρόν σενάριο εισάγουμε τους μαθητές στην εκθετική συνάρτηση με τη βοήθεια ενός προβλήματος. Με τη βοήθεια κατάλληλου λογισμικού και αντίστοιχου φύλλοy εργασίας, οι μαθητές μπορούν να μοντελοποιήσουν σχετικά εύκολα το πρόβλημα. Όπως γνωρίζουμε η μοντελοποίηση φαινομένων και καταστάσεων είναι μια διαδικασία η οποία δεν είναι οικεία στους μαθητές και ως εκ τούτου αρκετές φορές είναι επίπονη. Επειδή ο απώτερος στόχος μας είναι η εξαγωγή συμπερασμάτων από αυτή τη διαδικασία, εκτιμούμε ότι ο προτεινόμενος σχεδιασμός προσφέρει κάτι τέτοιο και οδηγεί τον μαθητή στον δρόμο που θέλουμε χωρίς χρονοβόρες παρεκκλίσεις.
Για την ισχυροποίηση του ορισμού της εκθετικής οι μαθητές θα εργαστούν σε σχετικό αρχείο για τη δημιουργία δύναμης με άρρητο εκθέτη. Το αρχείο είναι σε λογισμικό Excel, αλλά δεν απαιτείται τίποτε παραπάνω από τους μαθητές όσον αφορά τη χρήση του λογισμικού, από το να μπορούν να πληκτρολογήσουν. “Απαιτείται” όμως από αυτούς να γνωρίζουν τα βασικά δομικά στοιχεία από τα οποία αποτελείται μια δύναμη, όπως εδώ η αx..
Στη συνέχεια αφού οι μαθητές “γνωρίσουν” την εκθετική συνάρτηση, βλέπουν μια αναφορά με παραδείγματα από την καθημερινότητα τα οποία μοντελοποιούνται με τη βοήθεια αυτής της συνάρτησης και τα οποία θα βοηθήσουν και στην εισαγωγή του αριθμού e.
Ακολουθεί η μελέτη της εκθετικής συνάρτησης (όπου αποφεύχθηκε η αναφορά στις ασύμπτωτες διότι εκτιμούμε ότι είναι μια έννοια η οποία θα απαιτούσε περισσότερη εμβάθυνση) και τέλος οι μαθητές καλούνται να λύσουν ανισώσεις και εξισώσεις εκθετικών συναρτήσεων, τις οποίες λύσεις κάθε φορά πρέπει να νοηματοδοτούν και μέσα από τις γραφικές παραστάσεις
Η μέθοδος διδασκαλίας που προτείνουμε να ακολουθηθεί είναι καθοδηγούμενη ανακάλυψη με ομαδοσυνεργατική μάθηση και χρήση ΤΠΕ.
Προαπαιτούμενα
Γνωστικό αντικείμενο
Έννοια συνάρτησης
Εύρεση πεδίου ορισμού
Εύρεση συνόλου τιμών μέσα από τη γραφική παράσταση
Ιδιότητες δυνάμεων (μέχρι και ρητούς εκθέτες)
Γραφική επίλυση εξίσωσης – ανίσωσης
Τεχνικό επίπεδο (λογισμικό Geogebra)
Κουτί εισαγωγής
Κίνηση δρομέα (με κέρσορα, ποντίκι, ενεργή κίνηση)
Εισαγωγή συναρτήσεων
Ορισμός σημείων τομής
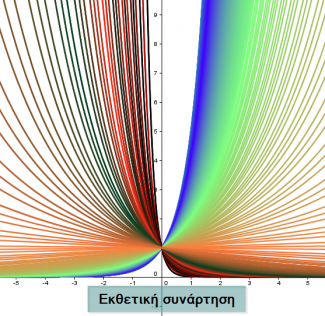
Η εισαγωγή στην εκθετική συνάρτηση γίνεται στο σχολικό βιβλίο με καθαρά αλγεβρικές διαδικασίες αφού πρώτα γίνει το πέρασμα από δυνάμεις με ρητό εκθέτη σε δυνάμεις με άρρητο εκθέτη. Ως γνωστό, οι αλγεβρικές διαδικασίες δεν είναι εύκολα νοηματοδοτούμενες, λόγω έλλειψης αναπαραστάσεων.Υπάρχει μια υπενθύμιση για τις δυνάμεις με ρητό εκθέτη (οι μαθητές τις έχουν διδαχτεί στην Α Λυκείου) και η δύναμη με άρρητο εκθέτη παρουσιάζεται με αλγεβρικές διαδικασίες και με λίγα (εξ ανάγκης) αριθμητικά παραδείγματα ως το όριο μιας ακολουθίας δυνάμεων που οι εκθέτες είναι δεκαδικές προσεγγίσεις του άρρητου εκθέτη., καταλήγοντας στο συμπέρασμα ότι «οι όροι της ακολουθίας φαίνεται (;) να προσεγγίζουν έναν συγκεκριμένο αριθμό». Οι μαθητές απλά παρατηρούν και “αναγκάζονται” να πειστούν. Όμως οι οριακές διαδικασίες μπορεί να γίνονται αντιληπτές στη φαντασία κάποιων μαθητών, αλλά σίγουρα δεν αποτελούν εύπεπτη τροφή για το μυαλό της πλειοψηφίας των μαθητών μιας συνηθισμένης τάξης. Στον αντίποδα των παραπάνω, είναι κοινώς αποδεκτό ότι η διδασκαλία μπορεί να έχει πολλά θετικά αποτελέσματα όταν αυτή γίνεται οπτικο –ενεργά.
Από την άλλη μεριά, η έννοια της συνάρτησης από μόνη της είναι μια προβληματική έννοια για αρκετούς μαθητές. Παρουσιαζόμενη η εκθετική συνάρτηση με τον τυπικό τρόπο της απεικόνισης δεν φαίνεται να βοηθάει ιδιαίτερα τα πράγματα. Η κατασκευή δε της γραφικής της παράστασης γίνεται επίσης με έναν τρόπο στατικό, με την κατασκευή ενός εκ των πραγμάτων περιορισμένου πίνακα τιμών που οι μαθητές πρέπει να φανταστούν την απεικόνιση των σημείων που αυτός παριστάνει, στο καρτεσιανό επίπεδο. Ανάλογη τύχη έχει και η μονοτονία της.
Επιπλέον, κατά κατά την άποψή μας, η εφαρμογή της μονοτονίας και του 1–1 στη λύση ανισώσεων και εξισώσεων, που είναι ένα από τα απαιτητά αλγεβρικά στοιχεία που πρέπει να γνωρίζουν οι μαθητές, δεν αντιμετωπίζεται με επιπλέον νοηματοδότηση από τους μαθητές.
Βιντεοπροβολέας
Σύνδεση στο Internet
Πίνακας για σημειώσεις
Υπολογιστές σε δίκτυο (για αποθήκευση εργασιών και έλεγχο προόδου εργασιών)
Δημιουργός Σεναρίου: ΜΑΡΙΟΣ ΣΠΑΘΗΣ (Εκπαιδευτικός)
Έλεγχος Σεναρίου με τα Προγράμματα Σπουδών: ΚΕΙΣΟΓΛΟΥ ΣΤΕΦΑΝΟΣ (Σχολικός Σύμβουλος)
Έλεγχος Επιστημονικής Επάρκειας Σεναρίου: ΣΚΟΥΡΑΣ ΑΘΑΝΑΣΙΟΣ (Συντονιστής)