Το Πυθαγόρειο θεώρημα και το αντίστροφό του. Εφαρμογή τους σε δυο ενδιαφέροντα προβλήματα.
Μαθηματικά (ΔΕ) (Γυμνάσιο)
Το Πυθαγόρειο θεώρημα και το αντίστροφό του. Εφαρμογή τους σε δυο ενδιαφέροντα προβλήματα.
Όπως αναφέρει ο Τριανταφύλλου (2008, σελ.15): “ Σήμερα σκεφτόμαστε το Πυθαγόρειο Θεώρημα ως αλγεβρική σχέση, από την οποία το μήκος μιας πλευράς ενός ορθογωνίου τριγώνου μπορεί να βρεθεί λαμβάνοντας υπόψη τα μήκη των άλλων δύο πλευρών.
Ο Πυθαγόρας δεν την αντιλήφθηκε έτσι. Γι’ αυτόν ήταν μια γεωμετρική δήλωση για τα εμβαδά ενώ με την ανάπτυξη της σύγχρονης άλγεβρας, περίπου το 16ο αιώνα, το Θεώρημα εξοικειώθηκε στην αλγεβρική του μορφή (Heath, 1956). Αυτό είναι σημαντικό να αντέξει στο μυαλό μας, επισημαίνοντας την εξέλιξη του Θεωρήματος κατά τη διάρκεια των 2.500 ετών από τότε που ο Πυθαγόρας υποθετικά το απέδειξε πρώτος και το έκανε αθάνατο. Δεν ήταν, πιθανόν, ούτε καν ο πρώτος που ανακάλυψε το Θεώρημα. Ήταν γνωστό στους Βαβυλώνιους και ενδεχομένως στους Κινέζους, τουλάχιστον χίλια έτη πριν από αυτόν (Van der Waerden, 2000)”.
Επομένως, δυσκολίες εντοπίζονται στην προσπάθεια των μαθητών να “ξεπεράσουν” την αλγεβρικότητα της σχέσης και να την συνδέσουν με την έννοια του εμβαδού και την εφαρμογή της σε θέματα γεωμετρίας και επιφανειών. Δυσκολίες υπάρχουν όταν προσπαθούν να θυμούνται και να χρησιμοποιούν τύπους χωρίς να τους έχουν συνδέσει ή κατασκευάσει μέσω δραστηριοτήτων.
Διδακτικά εμπόδια εντοπίζονται από τη στατικότητα των σχημάτων με τον παραδοσιακό τρόπο διδασκαλίας με κιμωλία και ειδικότερα της εικασίας αλλά μετέπειτα και της αποδεικτικής διαδικασίας του Πυθαγορείου θεωρήματος.
Έτσι, μέσω αυτού του σεναρίου:
Επιχειρούμε να δώσουμε τη δυνατότητα στους μαθητές να διατυπώσουν και ερμηνεύσουν γεωμετρικά το Πυθαγόρειο θεώρημα και το αντίστροφό του, αφού πρώτα παρατηρήσουν σχέσεις εμβαδών, υποθέσουν για τη γενίκευσή τους και εικάσουν τη σχέση τους.
Παράλληλα οι μαθητές να εντοπίσουν και εφαρμόσουν σε συγκεκριμένα παραδείγματα τη χρησιμότητά τους και ειδικότερα σε δυο προβλήματα που θα τους τραβήξουν το ενδιαφέρον, με επίκεντρο εκείνο, της εύρεσης ελάχιστης απόστασης μιας μύγας από μια αράχνη.
Οι μαθητές χρησιμοποιώντας τα εργαλεία του λογισμικού, τη δυναμική κίνηση που παρέχει και τις πολλές δυνατότητες εμπλοκής και αλλαγής στοιχείων και παραμέτρων, θα καταστούν ικανοί να διατυπώσουν μόνοι τους το Πυθαγόρειο θεώρημα και το αντίστροφο, να εικάσουν τη γενικότητά του και να το αποδείξουν δυναμικά μέσα από διαδικασίες συνεργασίας και ανταλλαγής απόψεων. Οι ίδιοι καταγράφουν μετρήσεις, παρατηρούν και αποφασίζουν για τα αποδεικτικά βήματα που θα ακολουθήσουν. Καλούνται έτσι να “μάθουν” την αντίστοιχη γεωμετρική γνώση μέσα από την παρατήρηση και να έχουν μάλιστα εμπλοκή με περισσότερες από μια αποδεικτικές διαδικασίες, που, στο επίπεδο του Γυμνασίου, είναι δύσκολο να κατανοηθούν χωρίς το δυναμικό μετασχηματισμό του σχήματος.
Τέλος, να αναφέρουμε ότι είναι σημαντικό τα προβλήματα που δίνονται για να εργαστούν οι μαθητές, πρέπει σύμφωνα με το National Research Council και πλήθους άλλων ερευνητών της διδακτικής των Μαθηματικών, να είναι προκλητικά στη σκέψη και να αντιμετωπίζονται με δεδομένα και παρατηρήσεις από τον πραγματικό κόσμο.
Βιβλιογραφία
Heath, T.L. (1956). The Thirteen Books of Euclid’s Elements. New York: Dover.
Μaor, E. (2007). The Pythagorean Theorem. New Jersey: Princeton University Press.
National Research Council. (2001). Adding it up: Helping children learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell (Eds). Mathematics Learning Subcommittee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington DC: National Academy Press.
Τριανταφύλλου, Δ. (2008). Μια μελέτη για τη διδασκαλία του Πυθαγορείου Θεωρήματος μέσω της θεωρίας των ενσώματων μαθηματικών (Embodied Mathematics). Δημοσιευμένη Διπλωματική εργασία), Διαπανεπιστημιακό – Διατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών “ΔΙΔΑΚΤΙΚΗ ΚΑΙ ΜΕΘΟΔΟΛΟΓΙΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ”, Αθήνα.
Van Der Waerden, B.L. (2000). Η Αφύπνιση της Επιστήµης. (Γ. Χριστιανίδη, µετάφραση). Ηράκλειο: Πανεπιστηµιακές Εκδόσεις Κρήτης. (Πρωτότυπη έκδοση, 1954).
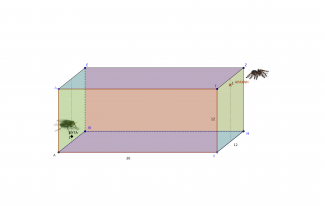
Η διατύπωση και γεωμετρική ερμηνεία του Πυθαγορείου θεωρήματος και του αντιστρόφου του, με παρατήρηση σχέσεων εμβαδών, υποθέσεις γενίκευσης και εικασίες σχέσεων.
Παράλληλα, η εφαρμογή σε συγκεκριμένα παραδείγματα και προβλήματα για τη χρησιμότητά τους και ειδικότερα σε δυο ενδιαφέροντα προβλήματα, με επίκεντρο εκείνο, της εύρεσης ελάχιστης απόστασης μιας μύγας από μια αράχνη.
Δημιουργός Σεναρίου: ΚΩΝΣΤΑΝΤΙΝΟΣ ΖΥΓΟΥΡΗΣ (Εκπαιδευτικός)