Αντιστρόφως ανάλογα ποσά
Μαθηματικά (ΔΕ) (Γυμνάσιο)
Το συγκεκριμένο σενάριο περιλαμβάνει την εισαγωγή στα αντιστρόφως ανάλογα ποσά σε μαθητές Α γυμνασίου. Μπορεί όμως κάλλιστα ένα μέρος του (φάση 2) να χρησιμοποιηθεί και για εισαγωγή σε έννοιες σχετικές με τα κλάσματα και τα ισοδύναμα κλάσματα.
Οι μαθητές, χωρισμένοι σε ομάδες των δυο ατόμων (σε περίπτωση αδυναμίας χρήσης της αίθουσας υπολογιστών, μπορεί να χρησιμοποιηθεί η σχολική τάξη με έναν βιντεοπροβολέα), πειραματίζονται με κατάλληλες δραστηριότητες σχεδιασμένες στο περιβάλλον του geogebra.Το συγκεκριμένο περιβάλλον τους δίνει τη δυνατότητα, μέσα από προσεκτικά σχεδιασμένα προβλήματα και δραστηριότητες, να κάνουν υποθέσεις και εικασίες, να τις ελέγχουν, να παρατηρούν ένα μοντέλο, να ασχοληθούν με την έννοια της ταυτόχρονης μεταβολής δυο μεγεθών και τη δυναμική διασύνδεση των πολλαπλών αναπαραστάσεων της ίδιας έννοιας. Η θεωρία μάθησης που υιοθετείται, είναι αυτή της μάθησης μέσω κατασκευών. Η συγκεκριμένη θεωρία ισχυρίζεται ότι η διαδικασία μάθησης στα Μαθηματικά είναι μια κατασκευαστική δραστηριότητα όπου ο μαθητής συμμετέχει ενεργά στην κατασκευή της γνώσης.
Μέσα από την επίλυση του προβλήματος:
1) εύρεσης ορθογωνίων σταθερού εμβαδού μεταβλητών διαστάσεων και
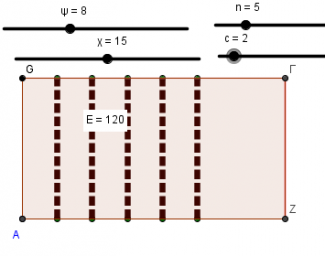
2) της ισοδιαμέρισης ενός ορθογωνίου σταθερών διαστάσεων στο περιβάλλον του geogebra,
οι μαθητές θα προσδιορίσουν, για τα διάφορα εμπλεκόμενα μεγέθη, σχέσεις αντιστρόφως αναλόγων ποσών, και θα προβούν στην κατασκευή πίνακα τιμών και των γραφικών αναπαραστάσεων.
Ο ρόλος του εκπαιδευτικού είναι αυτός του διευκολυντή της μάθησης, επιβλέπει με τρόπο διακριτικό, συμβουλεύει, συζητά ή και θέτει προβλήματα προς διερεύνηση, συμμετέχει στην αντιμετώπιση και επίλυση αποριών που ανακύπτουν, ενθαρρύνει τις ομάδες, παρακολουθεί και αξιολογεί την όλη διαδικασία, με στόχο αυτές να κινούνται μέσα στο προκαθορισμένο βάσει του σχεδίου πλαίσιο.
Η έννοια της αναλογίας (ευθεία και αντίστροφη) αποτελεί μια από τις σημαντικότερες έννοιες που συναντούν οι μαθητές σε όλες τις βαθμίδες εκπαίδευσης, ιδιαίτερα δε στις πρώτες τάξεις του γυμνασίου, και οι σχετικές έρευνες έχουν αναδείξει την ύπαρξη σημαντικών προβλημάτων που αντιμετωπίζουν οι μαθητές τόσο στη διάκριση αυτών όσο και γενικότερα στην κατανόησή τους.
Στα σχολικά εγχειρίδια, πολλές φορές χρησιμοποιούνται γεωμετρικά προβλήματα (π.χ η περίπτωση του ορθογωνίου σταθερού εμβαδού μεταβλητών διαστάσεων) για την προσέγγιση εννοιών όπως αυτή των αντιστρόφως αναλόγων ποσών. Οι μαθητές του γυμνασίου αντιμετωπίζουν τα θέματα αυτά με στατικούς τρόπους και λεκτικές περιγραφές χωρίς να έχουν τη δυνατότητα να πειραματιστούν, να διερευνήσουν και να περιγράψουν τη συμμεταβολή των εμπλεκομένων μεγεθών. Επιπλέον δυσκολίες προκύπτουν από το γεγονός ότι η έννοια των αντιστρόφως αναλόγων ποσών είναι μια έννοια με πολλούς τρόπους αναπαράστασης. Έχει παρατηρηθεί, ότι οι μαθητές δυσκολεύονται γενικότερα τόσο στη διασύνδεση αυτών με τη χρήση των στατικών μέσων που συνήθως χρησιμοποιούνται στα σχολικά εγχειρίδια, αλλά και στην μετατροπή μιας αναπαράστασης σε μια άλλη ιδιαίτερα κατά τη διαδικασία επίλυσης προβλημάτων.
Ένα επίσης σημαντικό θέμα προκύπτει από τις περιορισμένες δυνατότητες που έχουν τα στατικά μέσα για την αναπαράσταση μιας καμπύλης. Σύμφωνα με τη Laborde (2010), η κατασκευή της γραφικής παράστασης στο περιβάλλον 'χαρτί-μολύβι', σε αντίθεση με τα δυναμικά εργαλεία όπως το geogebra, περιορίζεται στην αναπαράσταση μόνο μερικών σημείων τα οποία στη συνέχεια συνδέονται με μια ομαλή καμπύλη, αλλά οι μαθητές δεν έχουν ιδέα για το τι αυτή η καμπύλη παριστάνει.
Δημιουργός Σεναρίου: ΙΩΑΝΝΗΣ ΖΑΝΤΖΟΣ (Εκπαιδευτικός)
Έλεγχος Σεναρίου με τα Προγράμματα Σπουδών: ΚΕΙΣΟΓΛΟΥ ΣΤΕΦΑΝΟΣ (Σχολικός Σύμβουλος)
Έλεγχος Επιστημονικής Επάρκειας Σεναρίου: ΣΚΟΥΡΑΣ ΑΘΑΝΑΣΙΟΣ (Συντονιστής)