Μέτρηση του μήκους του κύκλου με προσέγγιση των περιμέτρων κανονικών πολυγώνων
Μαθηματικά (ΔΕ) (Γενικό Λύκειο)
Μέτρηση του μήκους του κύκλου με προσέγγιση των περιμέτρων κανονικών πολυγώνων
Στην ύλη της Γεωμετρίας της Β΄ Λυκείου η μέτρηση του κύκλου επιτυγχάνεται μέσω των κανονικών πολυγώνων. Το κοινό όριο των περιμέτρων, του εγγεγραμμένου κανονικού πολυγώνου στον κύκλο, του οποίου ο αριθμός των πλευρών αυξάνεται συνεχώς για να προσεγγίσει τον κύκλο εσωτερικά και του περιγεγραμμένου με αντίστοιχο αριθμό πλευρών κανονικού πολυγώνου στον κύκλο, του οποίου ο αριθμός των πλευρών αυξάνεται για να προσεγγίσει τον κύκλο εξωτερικά, μας δίνει το μήκος του κύκλου. Με αυτή τη διαδικασία, δηλαδή της συνεχόμενης αύξησης του αριθμού των πλευρών του εγγεγραμμένου και περιγεγραμμένου κανονικού πολυγώνου, οι μαθητές διαχειρίζονται τις επ’ άπειρον διαδικασίες μέσα από τις οποίες αναδεικνύεται ο αριθμός π.
Θα λέγαμε ότι η σπουδαιότερη προστιθέμενη αξία αυτού του σεναρίου είναι, ότι με τη μέθοδο των προσεγγίσεων των περιμέτρων των εγγεγραμμένων και περιγεγραμμένων κανονικών πολυγώνων περί του ίδιου κύκλου, οι μαθητές θα ανακαλύψουν ότι η προσέγγιση, είναι μέθοδος αντιμετώπισης προβλημάτων και μέθοδος απόδειξης και θα αναιρέσουν τις επιφυλάξεις που πιθανόν έχουν, ότι η προσέγγιση δεν αποτελεί αυστηρή μαθηματική διαδικασία.
Θα ανακαλύψουν το βασικό τύπο της Γεωμετρίας L=2πR , γιατί θα φτάσουν σ’ αυτόν μέσω της ακολουθούμενης διαδικασίας και έτσι θα τον εμπεδώσουν ευκολότερα.
Χρησιμοποιώντας το λογισμικό πολλαπλών δυναμικά συνδεδεμένων αναπαραστάσεων, οι μαθητές ανακαλύπτουν μόνοι τους τη σχέση που ζητάμε να αναγνωρίσουν και επιβεβαιώνουν ή όχι την εικασία που κάνουν οι ίδιοι στις αρχές των δραστηριοτήτων του σεναρίου, κάνοντας πειραματισμούς.Το κοινό φύλλο εργασίας και η κοινή οθόνη βοηθούν τους μαθητές να επικοινωνούν εντός της ομάδας τους. Μέσω της ομαδοσυνεργατικής διδασκαλίας ενεργοποιούμε τον κάθε μαθητή της ομάδας αναθέτοντάς του αντίστοιχη δραστηριότητα
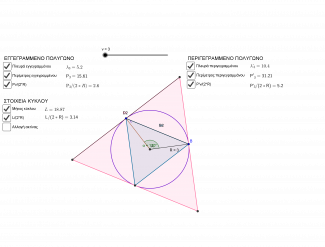
Στο συγκεκριμένο σενάριο δεν υπάρχει αφόρμηση. Καλούμαστε να διδάξουμε στη Γεωμετρία της Β' Λυκείου το μήκος του κύκλου με τη μέθοδο των διαδοχικών προσεγγίσεων. Σε αυτή τη μέθοδο διδασκαλίας το βασικό δομικό στοιχείο για την κατανόηση του προβλήματος από τους μαθητές, είναι η κατασκευή πολλών διαδοχικών και ευκρινώς κατασκευασμένων πολυγώνων εγγεγραμένων και περιγεγραμμένων του κύκλου. Η συγκεκριμένη κατασκευή , υστερεί στον πίνακα με τη χρήση των απλών γεωμετρικών οργάνων . Γενικά η κατασκευή γεωμετρικών σχημάτων, που είναι και η πρώτη προϋπόθεση για την λύση πολλών ασκήσεων, δυσκολεύει ορισμένες φορές τους μαθητές, κυρίως αν υπάρχει μεγάλη διαδοχή κατασκευών. Το λογισμικό σε αυτή την περίπτωση βοηθά και τελειοποιεί την κατασκευή. Όμως η έλλειψη εξοικείωσης των μαθητών με τις απαραίτητες εντολές του λογισμικού είναι επίσης ένα πρόβλημα στην ακολουθούμενη διδασκαλία, το οποίο όμως μπορεί να ελαχιστοποιηθεί δίνοντας έτοιμα στους μαθητές το σχήμα με τα βασικά στοιχεία του, καθώς και κατάλληλα κουμπιά ελέγχου. Με αυτή τη βοήθεια οι μαθητές εμπλουτίζουν τις παραστάσεις τους και με αυτόν τον τρόπο βελτιώνουν τις ικανότητές τους.
Το μάθημα θα γίνει στο εργαστήριο της Πληροφορικής με χρήση του λογισμικού Geogebra, το οποίο δίνει αυτοματοποιημένες μετρήσεις και δυναμική παραγωγή κανονικών πολυγώνων, οπότε η προσέγγιση του μήκους του κύκλου είναι αρχικά διαισθητική και επομένως οι μαθητές έρχονται σε επαφή με έναν νέο γι’ αυτούς τρόπο απόδειξης, των διαδοχικών προσεγγίσεων
Ο καθηγητής χωρίζει τους μαθητές σε ομάδες των τριών με τρόπο ώστε οι ομάδες να είναι ανομοιογενείς στη σύνθεσή τους (ως προς την επίδοση, τη συμπεριφορά Οι ομάδες εργάζονται στο εργαστήριο Πληροφορικής του σχολείου και απαντούν στις ερωτήσεις του φύλλου εργασίας συνεργαζόμενοι (οι μαθητές της ίδιας ομάδας).
Ο κάθε μαθητής αναλαμβάνει και έναν από τους τρεις ρόλους: Συντονιστής, καταγραφέας, χειριστής του Η/Υ, όπου ο συντονιστής οργανώνει την ομάδα, ο καταγραφέας χειρίζεται το φύλλο εργασίας και ο χειριστής του Η/Υ χειρίζεται το λογισμικό.
Οι Συντονιστές όλων των ομάδων συγκεντρώνονται στο τέλος της κάθε δραστηριότητας, συζητούν και καταλήγουν σε κοινά συμπεράσματα. Αν σε κάποιο σημείο δεν συμφωνούν τα αποτελέσματά τους, προσπαθούν να εντοπίσουν το λάθος. Αφού καταλήξουν σε ένα κοινό αποτέλεσμα συνεχίζουν στην επόμενη δραστηριότητα.
Ο καθηγητής ελέγχει τη ροή εργασιών των ομάδων και ρυθμίζει την ταχύτητα εξέλιξης της δραστηριότητας. Παρακολουθεί και συντονίζει τις ομάδες, παίζοντας το ρόλο του βοηθού. Βοηθάει στη χρήση του λογισμικού και υποδεικνύει, χωρίς να επεμβαίνει, και μόνο για να διευκολύνει τις ομάδες να ξεπεράσουν διάφορα προβλήματα και αδιέξοδα τα οποία μπορεί να συναντήσουν, δίνοντάς τους κατάλληλα ερεθίσματα. Καθοδηγεί τους μαθητές ώστε να αντιλαμβάνονται καλύτερα τα αποτελέσματά τους και τους ενθαρρύνει να συνεχίσουν τη διερεύνηση. Σε καμία περίπτωση δεν δίνει το αποτέλεσμα κάποιου ερωτήματος έτοιμο.
• Γεωμετρικά όργανα (διαβήτης, χάρακας, σχοινάκι)
• Φύλλο Εργασίας
-Αρχείο geogebra