Γραμμικά συστήματα 2x2 - Γεωμετρικές διασυνδέσεις
Μαθηματικά (ΔΕ) (Γενικό Λύκειο)
Στο παρόν σενάριο επιχειρούμε να συνδέσουμε άμεσα ένα γραμμικό σύστημα με τη γεωμετρική του αναπαράσταση. Με αυτόν τον τρόπο θα νοηματοδοτήσουμε και την επίλυση ενός γραμμικού παραμετρικού συστήματος.
Το κεφάλαιο των γραμμικών συστημάτων αντιμετωπίζεται ως ένα «εύκολο» κεφάλαιο από το σύνολο των μαθητών. Λίγη θεωρία και «διαδικαστικοί» μαθηματικοί τύποι είναι τα χαρακτηριστικά του. Εκτιμούμε, ως εκ τούτου, ότι προσφέρει τη δυνατότητα για περαιτέρω εμβάθυνση και αποσαφήνιση διαφόρων εννοιών.
Κατ’ αρχάς θα γίνει διερευνητικό στάδιο υπό μορφή ερωτήσεων, με στόχο να κατηγοριοποιήσουν μέσω και οπτικοποίησης οι μαθητές τις διάφορες καμπύλες σε γραμμικές και μη.
Οι μαθητές, στα διάφορα στάδια του σεναρίου, καλούνται να εναλλάσσονται μεταξύ των γνωστικών πλαισίων (αλγεβρικό και γεωμετρικό) σηματοδοτώντας τα αποτελέσματά τους και γενικεύοντας, όπου αυτό είναι δυνατόν, τα συμπεράσματά τους. Αυτό θα συνεπικουρείται, όπου κρίνεται απαραίτητο, από σχετικό λογισμικό στο οποίο οι μαθητές θα εργαστούν καθοδηγούμενοι από κατάλληλα φύλλα εργασίας.
Ιδιαίτερα με τη χρήση του εργαλείου «δρομέας» θα εισαχθούν κατ’ αρχάς ακούσια στη δημιουργία παραμετρικών εξισώσεων, αλλά και θα μπορέσουν να οπτικοποιήσουν την ταύτιση δύο ευθειών, δεδομένου του ότι πίσω από μια τέτοια ταύτιση κρύβεται η ανακλαστική ιδιότητα a~a, που είναι αρκετά δύσκολη στη νοηματοδότησή της.
Στο παρόν σενάριο δεν αντιμετωπίζεται το θέμα των οριζουσών, αλλά εάν ο διδάσκων κρίνει σκόπιμο (ή αναγκαίο) μπορεί να διδάξει την αντίστοιχη ενότητα πριν από την ενασχόληση των μαθητών με παραμετρικά συστήματα ή όπου αλλού επιθυμεί. (Ο χρόνος διδασκαλίας της ενότητας, δεν έχει προσμετρηθεί στη διάρκεια του σεναρίου)
Το σενάριο ολοκληρώνεται με εφαρμογές των γραμμικών συστημάτων σε σχετικά απλά προβλήματα, τα οποία όμως απαιτούν νοηματοδότηση βασιζόμενη και στο πλαίσιο αναφοράς του προβλήματος, από το οποίο δημιουργείται το εκάστοτε γραμμικό σύστημα.
Η μέθοδος διδασκαλίας που προτείνουμε να ακολουθηθεί είναι καθοδηγούμενη ανακάλυψη με ομαδοσυνεργατική μάθηση και χρήση ΤΠΕ.
Προαπαιτούμενα
Γνωστικό επίπεδο
- Οι εξισώσεις ευθείας y=αx+β, y=β, x=k
- Η εξίσωση αx+βy=γ
- Ο σχεδιασμός ευθείας στο επίπεδο
- Η έννοια της συνάρτησης
- Επίλυση συστημάτων με τη μέθοδο αντικατάστασης και τη μέθοδο των αντίθετων συντελεστών
Τεχνικό επίπεδο (λογισμικό Geogebra)
- Κίνηση δρομέα
- Πληκτρολόγηση συναρτήσεων
- Αλλαγή χρωματισμού και πάχους γραμμής
- Σχεδίαση ίχνους
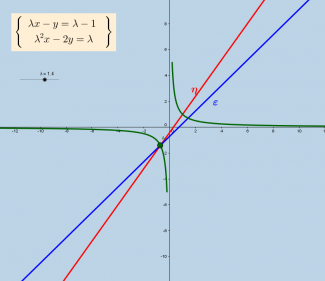
Ένα γραμμικό σύστημα βασίζεται σε δύο γραμμικές εξισώσεις. Η γραμμική εξίσωση αx+βy=γ έχει τρισυπόστατη μορφή.
- Είναι εξίσωση με δύο αγνώστους που επαληθεύεται στη γενική περίπτωση από άπειρα ζεύγη .
- Είναι (τις περισσότερες φορές) συνάρτηση
- Είναι ευθεία.
Οι μαθητές έχουν συνηθίσει από προηγούμενα χρόνια να δουλεύουν ως επί το πλείστον σε ένα καθαρά αλγεβρικό πλαίσιο και δύσκολα μπορούν να μεταφέρουν υποθέσεις ή συμπεράσματα από το αλγεβρικό στο γεωμετρικό πλαίσιο και τανάπαλιν.
Επιπρόσθετα, η ύπαρξη παραμέτρου δεν γίνεται αντιληπτή από τους μαθητές ως δημιουργός μιας οικογένειας συναρτήσεων και έτσι η επίλυση ενός παραμετρικού συστήματος σπάνια νοηματοδοτείται γεωμετρικά. Το αποτέλεσμα είναι η παραγωγή συμπερασμάτων, ορθών τις περισσότερες φορές τα οποία όμως (συμπεράσματα) συνήθως παραμένουν στο αρχικό πλαίσιο επεξεργασίας τους, χωρίς επιπλέον νοηματοδότηση.
Λογισμικό Geogebra εγκατεστημένο τοπικά
Βιντεοπροβολέας
Σύνδεση στο Internet
Πίνακας για σημειώσεις
Υπολογιστές σε δίκτυο (για αποθήκευση εργασιών και έλεγχο προόδου εργασιών)
Δημιουργός Σεναρίου: ΜΑΡΙΟΣ ΣΠΑΘΗΣ (Εκπαιδευτικός)
Έλεγχος Σεναρίου με τα Προγράμματα Σπουδών: ΚΕΙΣΟΓΛΟΥ ΣΤΕΦΑΝΟΣ (Σχολικός Σύμβουλος)
Έλεγχος Επιστημονικής Επάρκειας Σεναρίου: ΣΚΟΥΡΑΣ ΑΘΑΝΑΣΙΟΣ (Συντονιστής)