Οι τριγωνομετρικές συναρτήσεις και οι εφαρμογές τους
Μαθηματικά (ΔΕ) (Γενικό Λύκειο)
Το παρόν σενάριο αφορά τη διδασκαλία των τριών τριγωνομετρικών συναρτήσεων y=ημχ, y=συνχ, y=εφχ και ασχολείται με τρία κυρίως θέματα:
- τη μετάβαση από τον υπολογισμό των τριγωνομετρικών αριθμών ως λόγο πλευρών ορθογωνίου τριγώνου στην εισαγωγή των τριγωνομετρικών συναρτήσεων, μέσω της ιστορικής εξέλιξης της τριγωνομετρίας
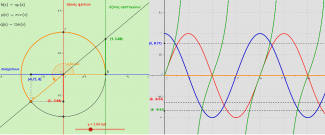
- τον ορισμό και τη μελέτη των τριγωνομετρικών συναρτήσεων μέσω του τριγωνομετρικού κύκλου και διερεύνησης μέσω δυναμικών πολλαπλών αναπαραστάσεων με το λογισμικό δυναμικής γεωμετρίας Geogebra
- τις εφαρμογές των τριγωνομετρικών συναρτήσεων στη μοντελοποίηση περιοδικών φαινομένων
Φάση 1
Στη φάση αυτή θα μελετήσουμε τόσο την ιστορική γέννηση των τριγωνομετρικών εννοιών όσο και του τρόπου που αυτές αναδομήθηκαν εξελισσόμενες κάτω από συγκεκριμένες ιστορικές και κοινωνικές συνθήκες. Η αναδρομή αυτή θα δώσει τη δυνατότητα στους μαθητές να κατανοήσουν πως οι τριγωνομετρικές έννοιες εξελίχθηκαν μέσα στο χρόνο: από τον ορισμό των τριγωνομετρικών αριθμών ως λόγο πλευρών ορθογωνίου τριγώνου από τους αρχαίους Αιγυπτίους και την κατασκευή πυραμίδων στη μελέτη χορδών κυκλικών τόξων από τους Έλληνες (όπου οι γωνίες δεν είναι πλεον μόνο οξείες) και τους σύγχρονους ορισμούς που χρησιμοποιούν την ημιχορδή.
Η ιστορική αναδρομή θα βοηθήσει ουσιαστικά τους μαθητές να κατανοήσουν την εισαγωγή του τριγωνομετρικού κύκλου και τον ορισμό των τριγωνομετρικών συναρτήσεων μέσω αυτού, που θα ακολουθήσει.
Φάση 2
Οι πρώτοι καταγεγραμμένοι πίνακες, όπως αναφέρθηκε, μελετούσαν τις μεταβολές των γωνιών. Χρησιμοποιώντας τον τριγωνομετρικό κύκλο και τις μεταβολές της γωνίας πάνω σε αυτόν, ορίζουμε την ημιτονοειδή συνάρτηση και στη συνέχεια τις συναρτήσεις του συνημιτόνου και της εφαπτομένης. Οι μαθητές πρέπει να καταλάβουν τις τριγωνομετρικές συναρτήσεις σαν μια διαδικασία, που παίρνει μια γωνία και την απεικονίζει σε έναν πραγματικό αριθμό. Η αντιστοίχιση της γωνίας χ στο ημχ γίνεται δυναμικά και μέσα από πίνακες τιμών και τη γραφική της παράσταση γίνεται η μελέτη της, όπου μελετώνται το πεδίο ορισμού της, το σύνολο τιμών της, η μονοτονία, τα ακρότατα κτλ. Κυρίως όμως διαφαίνεται καθαρά πλέον η περιοδικότητά της. Οι μαθητές με τη βοήθεια του λογισμικού δυναμικής γεωμετρίας Geogebra δημιουργούν μόνοι τους, διερευνούν δυναμικά και κατασκευάζουν την ημιτονοειδή συνάρτηση μεταβάλλοντας γωνίες.
Στη φάση αυτή αρχικά ορίζουμε εκ νέου τους τριγωνομετρικούς αριθμούς, ώστε να εφαρμόζονται για οποιοδήποτε γωνία πέραν της οξείας και γίνεται ιδιαίτερη αναφορά στην αναγκαιότητα χρήσης του ακτινίου για τη μέτρηση των γωνιών. Με τη χρήση των ακτινίων, οι τριγωνομετρικές συναρτήσεις παρουσιάζονται μέσω της κανονικής απεικόνισης του R στον τριγωνομετρικό κύκλο. Δηλαδή ο τριγωνομετρικός κύκλος θεωρείται ένας διπλωμένος άξονας αριθμών και έτσι η απεικόνιση του χ στο ημχ, με χ να είναι πραγματικός αριθμός, είναι πιο ορατή στους μαθητές.
Φάση 3
Οι μαθητές, μέσω πειραματισμών με το Geogebra, μετασχηματίζουν συναρτήσεις της μορφής y=ρημωx, y=ρημωx με ρ,ω>0 μεταβάλλοντας παραμέτρους, διερευνούν και παράγουν νέες υποθέσεις για απόδειξη. Συγκρίνουν τις γραφικές παραστάσεις που προκύπτουν με την y=ημx και βρίσκουν την περίοδο και το σύνολο τιμών τους.
Φάση 4
Οι τριγωνομετρικές συναρτήσεις,δεν έχουν μόνο όμορφα γραφήματα αλλά έχουν και πολυάριθμες πρακτικές εφαρμογές. Είναι εξαιρετικά χρήσιμες γιατί μπορούν να απεικονίσουν πολλά φυσικά φαινόμενα, από την κίνηση των θαλάσσιων κυμάτων μέχρι τη διάδοση του φωτός και από τις ταλαντώσεις της μεμβράνης του τυμπάνου μέχρι τις μεταβολές δυναμικού του οικιακού ρεύματος.
Οι μαθητές βλέπουν κάποιες πραγματικά εντυπωσιακές εφαρμογές των τριγωνομετρικών συναρτήσεων και επιλύουν πραγματικά προβλήματα.
Οργάνωση της τάξης
Σε όλες τις φάσεις του σεναρίου οι μαθητές εργάζονται ομαδικά στο εργαστήριο πληροφορικής του σχολείου, διερευνούν και εξάγουν συμπεράσματα προς απόδειξη, καθοδηγούμενοι από έντυπα φύλλα εργασίας και φυσικά τον εκπαιδευτικό. Εναλλακτικά, κάποιες από τις δραστηριότητες μπορούν να πραγματοποιηθούν στην τάξη με τη χρήση βιντεοπροβολέα και φύλλων εργασίας.
Βιβλιογραφία
Bunt L.,Jones P., Bedient J. (1981). Οι ιστορικές ρίζες των στοιχειωδών μαθηματικών. Εκδόσεις Πνευματικός, Αθήνα.
C.C.Clawson (1999). Η μαγεία των μαθηματικών. Εκδόσεις Κέδρος, Αθήνα.
Ανδρεαδάκης Σ., Κατσαργύρης Β., Παπασταυρίδης Σ., Πολύζος Γ., Σβέρκος Α. (2012). Άλγεβρα Β΄Λυκείου.ΙΤΥΕ "Διόφαντος".
Λιναρδάκης Π. Η παρουσίαση των τριγωνομετρικών εννοιών στα σχολικά βιβλία συγκριτικά με την ιστορική τους εξέλιξη (από το Γυμνάσιο στο Λύκειο).
Μήλιος Γ.(2011). Μετάβαση από το ημω, 0ο<ω<90ο στο ημx, xΕR μέσω της χρήσης του λογισμικού Geogebra. Διπλωματική εργασία, Αθήνα.
Ιστοσελίδες
Σκοπός του σεναρίου είναι οι μαθητές να μεταβούν από τους τριγωνομετρικούς αριθμούς που έχουν οριστεί σαν λόγοι πλευρών ορθογωνίου τριγώνου στην έννοια της τριγωνομετρικής συνάρτησης και να κατανοήσουν ότι ο υπολογισμός τριγωνομετρικών αριθμών σε ορθογώνιο τρίγωνο δεν αποτελούσε μια αλγεβρική διαδικασία η οποία διδάχθηκε στο γυμνάσιο, αλλά αποτελεί τη βάση αλλά και το απαραίτητο εργαλείο για σύνδεση με την τριγωνομετρική συνάρτηση.
Οι μαθητές διδάσκονται πρώτη φορά στη Β' Γυμνασίου τους τριγωνομετρικούς αριθμούς ως λόγους πλευρών ορθογωνίου τριγώνου. Στη Β΄Λυκείου εισάγεται η έννοια της τριγωνομετρικής συνάρτησης μέσω των εφαρμογών της, όπως π.χ. της αρμονικής ταλάντωσης, όπου οι μαθητές αντιμετωπίζουν ιδιαίτερες δυσκολίες στο να κατανοήσουν πως μια στατική συμπεριφορά των τριγωνομετρικών αριθμών ξαφνικά μετατρέπεται σε συνάρτηση και πως το ημίτονο μιας οξείας γωνίας γίνεται ημίτονο πραγματικού αριθμού. Η δυσκολία στην αντιληπτική ικανότητα των μαθητών οφείλεται στην έλλειψη συνέχειας μεταξύ των δύο προσεγγίσεων και στο γεγονός ότι η ιστορική εξέλιξη αυτής της μετάβασης δεν γίνεται αντιληπτή λόγω της απότομης διακοπής από τον απλό υπολογισμό τριγωνομετρικών αριθμών σε ορθογώνια τρίγωνα, σε μελέτη τριγωνομετρικών συναρτήσεων.
Η αναφορά στην ιστορία της Τριγωνομετρίας έρχεται να συμβάλλει προς την κατεύθυνση της σύνδεσης των δύο κλάδων. Οι πίνακες χορδών (που είναι στην ουσία πίνακες ημιτόνων) δείχνουν τη συναρτησιακή σχέση γωνιών με τιμές χορδών. Η εξέλιξη στην ημιχορδή του διπλασίου τόξου αποτελεί γενίκευση του ορθογωνίου τριγώνου και των λόγων που ορίζονται σε αυτό.
Επίσης με το εκπαιδευτικό σενάριο, προσπαθούμε να υπερβούμε μια δεύτερη δυσκολία, αλλά εξίσου σημαντική, στην κατανόηση των τριγωνομετρικών συναρτήσεων. Αυτή οφείλεται στο γεγονός ότι οι μαθητές δυσκολεύονται να φανταστούν την εφαρμογή μιας διαδικασίας χωρίς να έχουν εμπλακεί σε αυτή. Η απόδειξη ενός αποτελέσματος προξενεί μεγαλύτερη αίσθηση όταν δημιουργείται από τους ίδιους τους μαθητές και δεν τους παρέχεται έτοιμο, προκύπτει από εμπειρικές παρατηρήσεις,πειραματισμούς και τη δυναμική διερεύνηση των στοιχείων της απόδειξης. Με βάση το γεγονός ότι οι τριγωνομετρικές συναρτήσεις μπορούν να κατανοηθούν καλύτερα σαν γεωμετρικές διαδικασίες, η χρήση νέων τεχνολογιών στη διδασκαλία της έννοιας είναι η καλύτερη επιλογή. Οι μαθητές πειραματίζονται και κατασκευάζουν τις τριγωνομετρικές συναρτήσεις μέσω της μεταβολής γωνιών στον τριγωνομετρικό κύκλο, εξάγουν και συζητούν τα συμπεράσματά τους.
Τέλος, σκοπός του σεναρίου είναι οι μαθητές να συνδέσουν τις μαθηματικές έννοιες και τις γνώσεις που απέκτησαν με την καθημερινότητα, αλλά και με άλλους επιστημονικούς κλάδους. Εξάλλου ένας από τους θεμελιώδεις στόχους της διδασκαλίας των μαθηματικών, είναι να προσφέρει τη δυνατότητα στους μαθητές να συσχετίσουν τις αφηρημένες ιδέες των μαθηματικών, με πραγματικές ή φυσικές καταστάσεις και να τους αποκαλύψει τη δύναμη αυτών ως ένα μέσο και εργαλείο για τη μελέτη και ερμηνεία του φυσικού κόσμου (Τουμάσης 1999). Οι εφαρμογές των τριγωνομετρικών συναρτήσεων παρουσιάζονται στο τελευταίο μέρος του σεναρίου με στόχο να διεγείρουν το ενδιαφέρον των μαθητών και να ολοκληρώσουν τη διδασκαλία της ενότητας.
Δημιουργός Σεναρίου: Μαρία Καλογήρου (Εκπαιδευτικός)