Η γραμμική εξίσωση αx+βy=γ
Μαθηματικά (ΔΕ) (Γυμνάσιο)
Το παρόν σενάριο απευθύνεται σε μαθητές της Γ γυμνασίου και καλύπτει ολόκληρη την παράγραφο 3.1 : Η έννοια της γραμμικής εξίσωσης αx+βy=γ
Αποτελείται απο τρείς φάσεις, οι δύο πρώτεςέχουν διάρκειά περίπου 45 λεπτά η κάθε μία, ενώ η τρίτη περίπου 10 λεπτά.
Η α΄ φάση έχει τίτλο "η λύση μιας γραμμικής εξίσωσης" , υπάρχει ένα φύλλο εργασίας που αφορά ενσωματωμένο αρχείο λογισμικού δυναμικής αναπαράστασης και πολλά διαδραστικά εργαλεία της παρούσης πλατφόρμας. Ο γενικός σκοπός είναι οι μαθητές να θεωρήσουν τα x,y σαν αγνώστους-μεταβλητές τις οποίες αντικαθιστούν με τιμές που δίνονται σαν ζεύγη.Οι μαθητές γνωρίζουν ήδη ότι όταν έχουμε επαλήθευση έχουμε λύση της εξίσωσης, αλλά εδώ έχουμε απειρία λύσεων την οποία αντιμετωπίζουμε με την απεικόνιση των λύσεων σε ορθοκανονικό σύστημα αξόνων. Στην προσπάθεια αυτή γίνεται σαφές στους μαθητές ότι τα ζεύγη λύσεων της γραμμικής εξίσωσης βρίσκονται σε ευθεία και ότι κάθε σημείο της ευθείας επαληθεύει την εξίσωση.
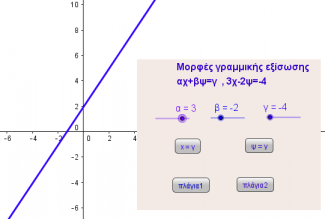
Η δεύτερη φάση έχει τίτλο:" η αναπαράσταση των λύσεων μιας γραμμικής εξίσωσης", υπάρχει επίσης ένα φύλλο εργασίας που αφορά ενσωματωμένο αρχείο λογισμικού δυναμικής αναπαράστασης και πολλά διαδραστικά εργαλεία της παρούσης πλατφόρμας.Το φύλλο εργασίας είναι απαραίτητο να ακολουθηθεί κατά γράμμα καθώς δίνει την δυνατότητα της καθοδήγησης του μαθητή.Αυτό γιατί ο μαθητής πρέπει να διακρίνει τριών ειδών ευθείες: κατακόρυφες, οριζόντιες και πλάγιες
η τρίτη φάση έχει τίτλο: "βρες το τετράγωνο" και αποτελεί στην ουσία ένα διαδραστικό παιχνίδι, όπου ο μαθητής προσπαθεί να δημιουργήσει ένα τετράγωνο που θα περικλείει ένα δεδομένο τετράγωνο και θα έχει εμβαδό τετραπλάσιο απο αυτό.
Τα αρχεία λογισμικού είναι κατάλληλες εφαρμογές του ελεύθερου λογισμικού geogebra είναι τέσσερα στο πλήθος,δύο για την α΄φάση, ένα για την β΄φάση και ένα διαδραστικό παιχνίδι για την τελευταία φάση.
Ενώ η διάδραση με το λογισμικό δίνει τη δυνατότητα στους μαθητές να δημιουργήσουν και να εξερευνήσουν, η εμπέδωση και αξιολόγηση των διαδράσεων και των στόχων του σεναρίου γίνονται μέσα απο τα ποικίλα δομικά διαδραστικά εργαλεία που παρέχει η παρούσα πλατφόρμα.Αυτά αφορούν ερωτήσεις κλειστού τύπου: πολλαπλής επιλογής, σωστού λάθους, καρτελλών, διαδραστικών παρουσιάσεων, ερωτήσεων αντιστοίχισης κλπ.Στο τέλος ένα διαδραστικό παιχνίδι δίνει τη δυνατότητα στους μαθητές να πληκτρολογήσουν ευθείες που σκοπός είναι να σχηματίσουν ένα τετράγωνο με συγκεκριμένες απαιτήσεις.
Τα φύλλα εργασίας συνοδεύουν κάθε φάση και κάθε δραστηριότητα που εμφανίζεται στο παρόν σενάριο, εκτυπώνονται και οι μαθητές σημειώνουν πάνω σε αυτά όλες τις πιθανές τους αλλά και τις διορθωμένες τους απαντήσεις.
Το μάθημα της γραμμικής εξίσωσης αx+βy=γ είναι ένα απο τα πλέον απαιτητικά για τη διδασκαλία του. Αυτό γιατί απαιτούνται πολλαπλές αναπαραστάσεις εννοιών που πρέπει να ενισχυθούν με πρόσθετα εργαλεία διδασκαλίας και τον σωστό καθοδηγητικό ρόλο του διδάσκοντα.
Στην αρχή της διδασκαλίας του μαθήματος οι μεταβλητές x,y είναι άγνωστοι και η αx+βy=γ είναι εξίσωση και αναζητάμε λύσεις της. Συνεχίζει σαν μια αριθμητική παράσταση που εξετάζουμε αν αληθεύει ή όχι για κάποια ζεύγη τιμών. Καταλήγουμε όμως να θεωρούμε την αx+βy=γ σαν συνάρτηση όπου οι άγνωστοι x,y παίζουν τώρα τον ρόλο εξαρτημένης-ανεξάρτητης μεταβλητής και ακόμα επίσης τον ρόλο της τετμημένης και τεταγμένης. Αναπαρίσταται δε, με σημεία τα οποία οδηγούν σε ευθεία. Έχουμε δηλαδή αγνώστους, ζεύγη τιμών, σημεία, και τελικά ευθείες. Δηλαδή έχουμε αλγεβρική προσέγγιση, αριθμητική προσέγγιση και τελικά γεωμετρική προσέγγιση για την ίδια έννοια.
Οι μαθητές είναι δύσκολο να κατανοήσουν αυτές τις πολλαπλές νοηματοδοτήσεις που δίνουμε σε αυτή την έννοια. Όλα αυτά απαιτούν νοητικές μεταφορές που εκφράζονται εύκολα στο παρόν σενάριο αφού δίνει τη δυνατότητα πολλαπλών αναπαραστάσεων της γραμμικής εξίσωσης αx+βy=γ.
Η εξέλιξη του σεναρίου σε φάσεις με πολλές δυναμικές δραστηριότητες που παρέχονται από τις διαδράσεις με τα εργαλεία της παρούσας ψηφιακής πλατφόρμας. καθώς και με το δυναμικό χειρισμό που παρέχει το ελεύθερο λογισμικό geogebra, δίνουν τη δυνατότητα στον μαθητή με τη σωστή καθοδήγηση των φύλλων εργασίας και του καθηγητή, να αποσαφηνίσει πλήρως τις γραμμικές εξισώσεις.
Δημιουργός Σεναρίου: Αιμίλιος Βλάστος (Εκπαιδευτικός)