ΣΧΕΔΙΟ ΜΑΘΗΜΑΤΟΣ

Α. Ταυτότητα

Διδακτική ενότητα: Μαθηματικά κατεύθυνσης Β’ Λυκείου

Θέμα: «Διανύσματα: Έννοιες, Πράξεις, Ανάλυση, Συντεταγμένες»

• Διάνυσμα
• Ιδιότητες διανυσμάτων
• Πράξεις με διανύσματα
• Ανάλυση διανύσματος σε δύο Συνιστώσες
• Συντεταγμένες στο Επίπεδο

Βασική ιδέα: Η διδασκαλία του κεφαλαίου των διανυσμάτων με τον παραδοσιακό τρόπο στον πίνακα και η μελέτη από το σχολικό βιβλίο, είναι μία στατική διαδικασία που δεν επιτρέπει στους μαθητές την πλήρη κατανόηση της έννοιας του διανύσματος και την εφαρμογή του στη φύση.

Με το παρόν σχέδιο μαθήματος (σενάριο), η εκμάθηση των εννοιών των διανυσμάτων και των εφαρμογών τους, γίνεται με ανίχνευση – διερεύνηση διαθεματικής εφαρμογής – προσομοίωσης σε περιβάλλον εκπαιδευτικού λογισμικού, από τον ίδιο το μαθητή.

Ένα φύλλο εργασίας καθοδηγεί το μαθητή, με οδηγίες χρήσης της εφαρμογής και κατάλληλες ερωτήσεις, να ενεργεί στην εφαρμογή και να παρακολουθεί κινήσεις αντικειμένων προσομοιάζοντας φυσικές καταστάσεις, έτσι ώστε να ανακαλύπτει έννοιες, τις ομοιότητες και τις διαφορές τους, να τις συνδέει μεταξύ τους και να διατυπώνει τους αντίστοιχους κανόνες. Έτσι η μετωπική – δασκαλοκεντρική διδασκαλία μετατρέπεται σε μαθητοκεντρική – ανακαλυπτική διαδικασία με πρωταγωνιστή το μαθητή.

Τεχνολογικά εργαλεία: Όλες οι προς μάθηση έννοιες παρουσιάζονται με πέντε εφαρμογές του εκπαιδευτικού λογισμικού CAS GeoGebra, οι οποίες είναι κατασκευασμένες με τέτοιο τρόπο, ώστε ο μαθητής να τις χειρίζεται μόνο σύροντας ή επιλέγοντας αντικείμενα με το δείκτη του ποντικιού, χωρίς ιδιαίτερες γνώσεις χρήσης του λογισμικού.

Β. Σκεπτικό της δραστηριότητας

Καινοτομίες: Η γνωσιοθεωρητική προσέγγιση του μαθήματος γίνεται με σύγχρονες κοινωνικές και εποικοδομιστικές προσεγγίσεις, δηλαδή με δυναμικό τρόπο, απειρία μετασχηματισμών και πολλαπλές αναπαραστάσεις.

Ομαδοσυνεργατική δουλειά για τη διαπραγμάτευση των απόψεων και τελικών συμπερασμάτων από τους μαθητές.

Φύλλα εργασίας με προσεκτικά σχεδιασμένες οδηγίες χρήσης της εφαρμογής και ερωτήσεις.

Καθηγητής στο ρόλο του εξυπηρετητή της μάθησης του μαθητή, μέσα από το σχεδιασμό κατάλληλων περιβαλλόντων μάθησης και όχι στο ρόλο του πομπού γνώσεων, που συνήθως συμβαίνει στο περιβάλλον μιας παραδοσιακής τάξης.

Προστιθέμενη αξία: Με τη χρήση των εφαρμογών των εκπαιδευτικών λογισμικών κάθε ομάδα μαθητών θα αλληλεπιδράσει, θα μετασχηματίσει δυναμικά, θα διερευνήσει και θα ανακαλύψει τις εξής έννοιες:

• Έννοια διανύσματος: στο συμβατικό βιβλίο ο μαθητής διαβάζει και βλέπει στατικές εικόνες και σχήματα, ενώ στην εφαρμογή δημιουργεί κινήσεις στον ίδιο ή σε κάθετους δρόμους, παρακολουθεί τις κινήσεις δύο κινητών, εντοπίζοντας τις κατευθύνσεις τους και τα χαρακτηριστικά τους.    
• Ιδιότητες διανυσμάτων: Τα χαρακτηριστικά των διανυσμάτων (φορέας, φορά, μέτρο, συγγραμμικότητα, γωνία διανυσμάτων), η ισότητα και η αντίθεση, γίνονται κατανοητά με κινήσεις και αυξομειώσεις των μέτρων των διανυσμάτων πάνω σε παράλληλους φορείς, με διεπαφή μαθητή – προσομοίωσης.
• Πράξεις με διανύσματα: Ο μαθητής παρακολουθεί και συμμετέχει με κίνηση στην απόδειξη της γεωμετρική πρότασης που πρώτος ο Ήρων ο Αλεξανδρεύς απέδειξε αιώνες πριν. Μετατοπίζει διανύσματα, αυξομειώνει τα μέτρα διανυσμάτων, τα καθιστά διαδοχικά ή με κοινή αρχή και εντοπίζει το άθροισμά και τη διαφορά τους, με τη διαδοχικότητα ή τον κανόνα του παραλληλογράμμου. Επίσης δημιουργεί το γινόμενο αριθμού επί διάνυσμα και ανακαλύπτει τη σχέση του με το αρχικό διάνυσμα.
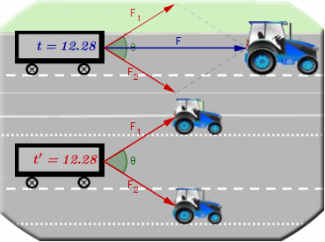
• Ανάλυση διανύσματος σε δύο Συνιστώσες: Ο μαθητής ανακαλύπτει τον τρόπο ανάλυσης ενός διανύσματος σε δύο συνιστώσες και παρακολουθεί εφαρμογή της ανάλυσης διανύσματος με επίδραση δυνάμεων επί του ίδιου αντικειμένου, το οποίο σε μία περίπτωση κινείται με την επίδραση μιας δύναμης και στην δεύτερη περίπτωση κινείται με την επίδραση δύο δυνάμεων και συγκρίνει, ανάλογα με τον χρόνο κάλυψης της ίδια απόστασης, τη συνισταμένη των δύο δυνάμεων με την πρώτη δύναμη.
• Συντεταγμένες στο Επίπεδο: Ο μαθητής με σύρσιμο του δείκτη του ποντικιού αντιλαμβάνεται τη δημιουργία του άξονα των πραγματικών αριθμών, τη δημιουργία του ορθοκανονικού συστήματος συντεταγμένων, εντοπίζει σημεία από διατεταγμένο ζεύγος συντεταγμένων, εντοπίζει τις συντεταγμένες τυχαίου σημείου του επιπέδου, κατασκευάζει με σύρσιμο διάνυσμα με αρχή την αρχή των αξόνων ίσο με δεδομένο διάνυσμα, ανακαλύπτει τις συντεταγμένες του, παρακολουθεί την κίνηση – στροφή του θετικού οριζόντιου ημιάξονα έως το διάνυσμα και διατυπώνει τον ορισμό του συντελεστή διεύθυνσης του διανύσματος.

Γνωστικά – διδακτικά προβλήματα: Γενικά όλες οι μαθηματικές έννοιες που απαιτούν πολλαπλές αναπαραστάσεις, είναι χρονοβόρες για τον διδάσκοντα και γίνονται δύσκολα κατανοητές από το μαθητή με την ανάγνωση και παρατήρηση των στατικών – πολύπλοκων εικόνων του βιβλίου.

Γ. Πλαίσιο εφαρμογής

Σε ποιους απευθύνεται: Το μάθημα απευθύνεται στους μαθητές της Β’ τάξης του Λυκείου.

Χρόνος υλοποίησης: Για την υλοποίηση του σεναρίου απαιτούνται επτά ή οκτώ διδακτικές ώρες περίπου.

Χώρος υλοποίησης: Προτείνεται οι μαθητές να εργαστούν εξ’ ολοκλήρου στο εργαστήριο υπολογιστών. Εναλλακτικά, το μάθημα μπορεί να γίνει σε αίθουσα με βιντεοπροβολέα, αλλά ο διδάσκων πρέπει να είναι κατάλληλα προετοιμασμένος, ώστε απευθυνόμενος στο σύνολο της τάξης, οι ερωτήσεις του να οδηγούν τους μαθητές στην ανακάλυψη των προς μάθηση εννοιών και διατύπωση των σχετικών κανόνων.

Προαπαιτούμενες γνώσεις των μαθητών: Σύνολο πραγματικών αριθμών,  καθετότητα – παραλληλία, γωνία, αριθμός π, εφαπτομένη γωνίας.

Απαιτούμενα βοηθητικά υλικά και εργαλεία:

• Τετράδιο για να κρατούν σημειώσεις κατά την πορεία της διερεύνησης, να καταγράφουν τα συμπεράσματά τους και να εκτελούν τις αλγεβρικές διαδικασίες όπου απαιτείται.
• Βιβλίο για να ανατρέχουν σε προηγούμενες έννοιες.
• Φύλλα εργασίας τα οποία δίνονται από τον διδάσκοντα και έχουν ως στόχο να καθοδηγούν τους μαθητές στη διερεύνηση - ανακάλυψη των προς μάθηση εννοιών και διατύπωση των σχετικών κανόνων.
• Κανόνα και διαβήτη για κατασκευές στο τετράδιο

Πριν την διεξαγωγή της δραστηριότητας ο διδάσκων μπορεί, μέσω απλών δραστηριοτήτων, να συζητήσει με τους μαθητές για τις βασικές λειτουργίες του λογισμικού αλλά και τις μαθηματικές έννοιες που απαιτούνται ως υπόβαθρο για την διεξαγωγή της.

Κοινωνική ενορχήστρωση της τάξης:

Οι μαθητές:

• Θα εργαστούν σε ομάδες των 3 ατόμων σε κάθε Η/Υ (ομαδοσυνεργατική μάθηση).
• Η σύνθεση κάθε ομάδας είναι ανομοιογενής ως προς την επίδοση στο συγκεκριμένο μάθημα, τις διαπροσωπικές σχέσεις των μαθητών, την κοινωνική  τους προέλευση και τη δυσκολία με την οποία εκδηλώνονται απέναντι σε καθηγητή, συμμαθητές.
• Ο ένας χειρίζεται την εφαρμογή, ο δεύτερος υπαγορεύει τις οδηγίες – ερωτήσεις  του φύλλου εργασίας, ο τρίτος παρακολουθεί τη σωστή εφαρμογή τους και όλοι μαζί συζητούν, αποφασίζουν και διατυπώνουν τις απαντήσεις. Φυσικά οι ρόλοι αυτοί μπορούν να εναλλάσσονται.
• Θα συμπληρώσουν ένα κοινό φύλλο εργασίας που περιέχει ερωτήσεις σχετικές με το θέμα. Μπορεί το φύλλο εργασίας να αφήνει μια σχετική ελευθερία στους μαθητές ώστε να θέτουν τα δικά τους ερωτήματα και να απαντούν σ’ αυτά.

Ο εκπαιδευτικός:

• Ελέγχει τα συμπεράσματα των μαθητών,
• Συνεργάζεται μαζί τους και τους καθοδηγεί ώστε να αντιλαμβάνονται καλύτερα τα αποτελέσματά τους
• Τους ενθαρρύνει να συνεχίσουν την διερεύνηση.

Τα τεχνολογικά εργαλεία:

Το εκπαιδευτικό λογισμικό CAS GeoGebra με το οποίο είναι κατασκευασμένες και οι πέντε εφαρμογές – προσομοιώσεις που χειρίζεται ο μαθητής, δίνει τη δυνατότητα άμεσης αλληλεπίδρασης του μαθητή με κάθε εφαρμογή ώστε να μετασχηματίζει και να δημιουργεί κατασκευές, να υποθέτει και να επαληθεύει τις υποθέσεις του, να κάνει μετρήσεις, να δίνει κίνηση σε αντικείμενα, κλπ.

Επέκταση του σεναρίου: Το σενάριο θα λέγαμε ότι αποτελεί ένα «πρότυπο» της ανακαλυπτικής μαθητοκεντρικής διδασκαλίας με χρήση Τ.Π.Ε. Με την ίδια φιλοσοφία μπορούμε να ανακαλύψουμε όλες τις έννοιες των μαθηματικών και της γεωμετρίας που απαιτούν σχήματα  και χρειάζονται πολλαπλές αναπαραστάσεις για να γίνουν κατανοητές.    

Βιβλιογραφία:

Κυνηγός Χρ. «Παιδαγωγική Αξιοποίηση των Ψηφιακών Τεχνολογιών για τη ∆ιδακτική των Μαθηματικών» (2007, Ελλ. Γράμματα).

Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Β’ Τάξης Ενιαίου Λυκείου

Ε. Αξιολόγηση μετά την εφαρμογή:

Ως προς τις επιδιώξεις του σεναρίου: Ο εκπαιδευτικός ελέγχει κατά πόσο επιτεύχθηκαν οι στόχοι του σεναρίου και εξετάζει του λόγους για τους οποίους κάποιοι δεν επιτεύχθηκαν ώστε να παρέμβει ανάλογα στο σενάριο.

Ως προς τα εργαλεία: Ο εκπαιδευτικός ελέγχει την ευκολία με την οποία οι μαθητές αξιοποίησαν τα εργαλεία του προτεινόμενου λογισμικού σε συνδυασμό με την σαφήνεια των οδηγιών και των περιγραφών των φύλλων εργασίας. Αφού αξιολογήσει τα δεδομένα του επεμβαίνει ανάλογα στο σενάριο για την επόμενη εφαρμογή.

Ως προς την διαδικασία υλοποίησης: Ο εκπαιδευτικός αξιολογεί την διαδικασία υλοποίησης του σεναρίου αξιολογώντας τα στοιχεία που δεν δούλεψαν καλά και αναπροσαρμόζει το σενάριο.

Ως προς την προσαρμογή και επεκτασιμότητα: Η δυνατότητα επέκτασης του σεναρίου και η ευκολία προσαρμογής σε ένα σχολικό περιβάλλον ή στην διδακτική ατζέντα ενός εκπαιδευτικού ή στην κουλτούρα μιας σχολικής τάξης είναι ένα από τα στοιχεία που το καθιστούν σημαντικό. Ο εκπαιδευτικός πρέπει να λάβει σοβαρά υπόψη του αυτές τις παραμέτρους και να προσαρμόσει το σενάριο ανάλογα. Ιδιαίτερα αν εφαρμόσει το σενάριο πολλές φορές και σε διαφορετικές τάξεις ή ανταλλάξει ιδέες με άλλους συναδέλφους του θα έχει δεδομένα με τα οποία θα μπορεί να κάνει ουσιαστικές προσαρμογές.